Skip to main content

[Python] __init__(클래스 생성자) & 이진트리 (정보처리기사 25년 1회 실기)


17. 다음은 파이썬에 대한 문제이다. 아래 코드를 확인하여 알맞는 출력값을 작성하시오.

class Node:
    def __init__(self, value):
        self.value = value
        self.children = []
 
def tree(li):
    nodes = [Node(i) for i in li]
    for i in range(1, len(li)):
        nodes[(i - 1) // 2].children.append(nodes[i])
    return nodes[0]
 
def calc(node, level=0):
    if node is None:
        return 0
    return (node.value if level % 2 == 1 else 0) + sum(calc(n, level + 1) for n in node.children)
 
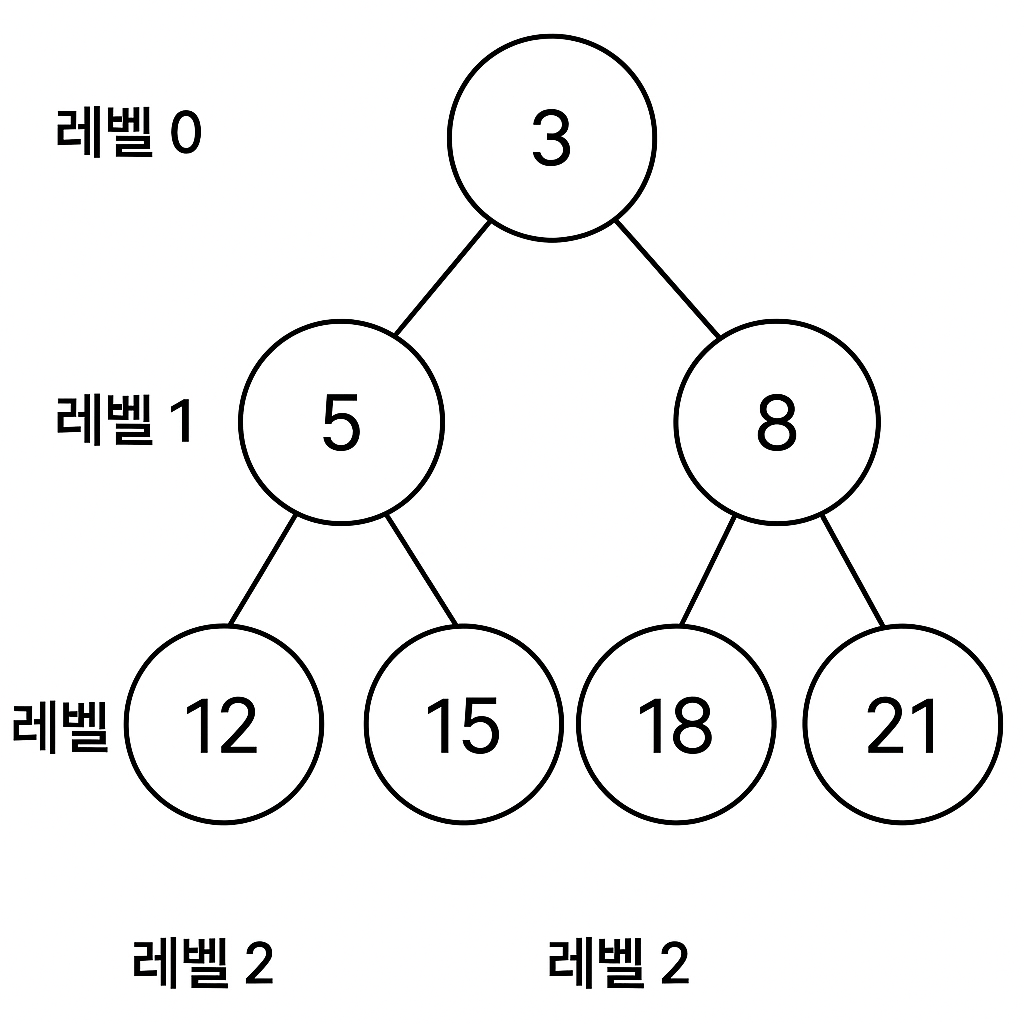
li = [3, 5, 8, 12, 15, 18, 21]
 
root = tree(li)
 
print(calc(root))
  • __init__: 객체가 만들어질 때 자동으로 실행되는 함수. Node 객체 생성 시 초기값 설정
  • children: 자식 노드들을 담는 리스트
  • tree(): 리스트를 기반으로 이진 트리를 구성하는 함수
  • calc(): 트리를 순회하면서 홀수 레벨 노드의 값을 합산하는 함수

정답: 13


왜 i는 1부터 시작할까?

li = [3, 5, 8, 12, 15, 18, 21]일 때 i = 0이면 nodes[(0 - 1) // 2] = nodes[-1]이 되기 때문에 오류가 나거나 엉뚱한 위치를 참조한다. nodes[0]은 루트 노드(root)로 사용되기 때문에, 부모가 없다. 그래서 연결할 필요도, 연결할 수 도 없다.


18, 21은 레벨 2인데, 왜 부모 인덱스가 2야? 부모 인덱스랑 레벨은 다른 개념이야?

부모 인덱스와 레벨은 완전히 다른 개념이다.

  • 부모 인덱스는 배열 내 규칙으로 계산되는 "부모 노드의 위치"
  • 레벨은 트리 상에서 "깊이(층수)"

용어

뜻

인덱스(index)

배열에서 요소의 위치 (0부터 시작)

레벨(level)

트리에서 루트로부터 몇 층 아래인지 나타내는 깊이 (0부터 시작)

  • index 3 (값 12)의 부모 인덱스는 1 → 값은 6
  • index 4 (값 15)의 부모 인덱스도 1 → 값은 6
  • index 5 (값 18)의 부모 인덱스는 2 → 값은 8
  • index 6 (값 21)의 부모 인덱스도 2 → 값은 8


if node is None: 이 무슨뜻이야?

  • 파이썬에서 None은 "값이 없음", **"아직 정해지지 않음"**을 나타내는 특별한 키워드이다.
  • if node is None: → "이 노드가 존재하지 않는다면" 체크하는 코드입니다.
  • 즉 이 코드는 node가 아무것도 없을 경우(=비어 있을 경우) 실행되는 코드이다.

트리에서 node는 일반적으로 어떤 노드를 가리킨다. 그런데 재귀 호출을 하다 보면, 어떤 노드에는 자식이 없을 수도 있다. 

3
   / \
  5   8
 / \
12 15

위의 노드 트리 구조에서 12와 15는 자식이 없다. 그러면 node.children은 빈 리스트이고, 그 아래는 없으니까 None인 경우가 생길 수 있다. 그럴 때 이 줄이 작동한다. 만약 node가 없으면 0을 리턴하고 있으면 node.value를 사용하라는 뜻이다. 

if node is None:
    return 0  # 아무것도 없으니 계산할 것도 없음


1. 클래스 Node 

class Node:
    def __init__(self, value):
        self.value = value       # 이 노드가 가지는 값
        self.children = []       # 이 노드의 자식 노드들 (리스트)
  • Node는 트리의 각 노드를 나타내는 클래스
  • value: 이 노드가 저장하는 숫자 값
  • children: 이 노드의 자식 노드들 (최대 2개 — 이진 트리)

[예시]

n = Node(3)
print(n.value)      # 3
print(n.children)   # []


2. 트리 생성 함수 tree()

def tree(li):
    nodes = [Node(i) for i in li]
    for i in range(1, len(li)):
        nodes[(i - 1) // 2].children.append(nodes[i])
    return nodes[0]
  • li 리스트를 바탕으로 Node 객체들을 만든 후,
  • 이진 트리 구조로 연결
  • [(i - 1) // 2]는 부모 인덱스 계산 공식이다.
예시: li = [3, 5, 8, 12, 15, 18, 21] 
index : value
0     : 3    → root
1     : 5    → 3의 왼쪽 자식
2     : 8    → 3의 오른쪽 자식
3     : 12   → 5의 왼쪽 자식
4     : 15   → 5의 오른쪽 자식
5     : 18   → 8의 왼쪽 자식
6     : 21   → 8의 오른쪽 자식

3. 계산 함수 calc()

def calc(node, level=0):
    if node is None:
        return 0
    return (node.value if level % 2 == 1 else 0) + sum(calc(n, level + 1) for n in node.children)
  • 자식 노드들을 재귀적으로 계산하는 코드이다.
  • level이 홀수(1, 3, ...)인 노드의 value만 더한다.
  • 아래 이 구조를 시각화한 트리에서 레벨 1인 value만 더하기 때문에 5 + 8 = 13image.png
Back to top