Skip to main content

43. [Java] 행렬의 곱셈

https://school.programmers.co.kr/learn/courses/30/lessons/12949

  • 2차원 행렬 arr1과 arr2를 입력받아, arr1에 arr2를 곱한 결과를 return
  • 행렬 arr1, arr2의 행과 열의 길이는 2 이상 100 이하이다.
  • 행렬 arr1, arr2의 원소는 -10 이상 20 이하인 자연수이다.
  • 곱할 수 있는 배열만 주어진다.

정답코드

class Solution {
    public int[][] solution(int[][] arr1, int[][] arr2) {
        int row1 = arr1.length;          // arr1의 행
        int col1 = arr1[0].length;       // arr1의 열 == arr2의 행
        int col2 = arr2[0].length;       // arr2의 열

        int[][] answer = new int[row1][col2]; // 결과 행렬의 크기

        // 행렬 곱셈
        for (int i = 0; i < row1; i++) {
            for (int j = 0; j < col2; j++) {
                for (int k = 0; k < col1; k++) {
                    answer[i][j] += arr1[i][k] * arr2[k][j];
                }
            }
        }

        return answer;
    }
}


행렬 곱셈의 전제 조건

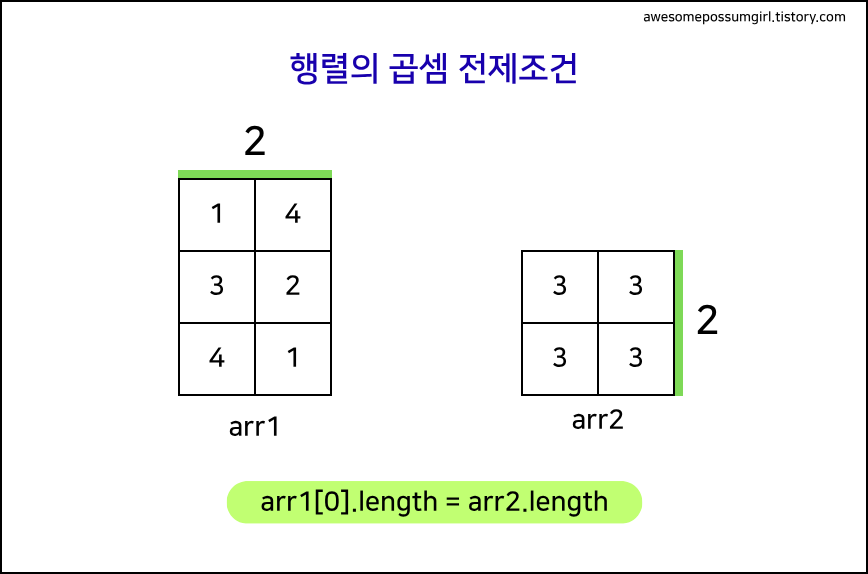
1 (4).png

행렬의 곱셈 결과.png

arr1의 열 개수 = arr2의 행 개수여야 한다.
👉 arr1[0].length == arr2.length
  • arr1은 3x2
  • arr2는 2x2
    → 이 경우 곱셈 가능 (2 = 2)

예를 들면 : 

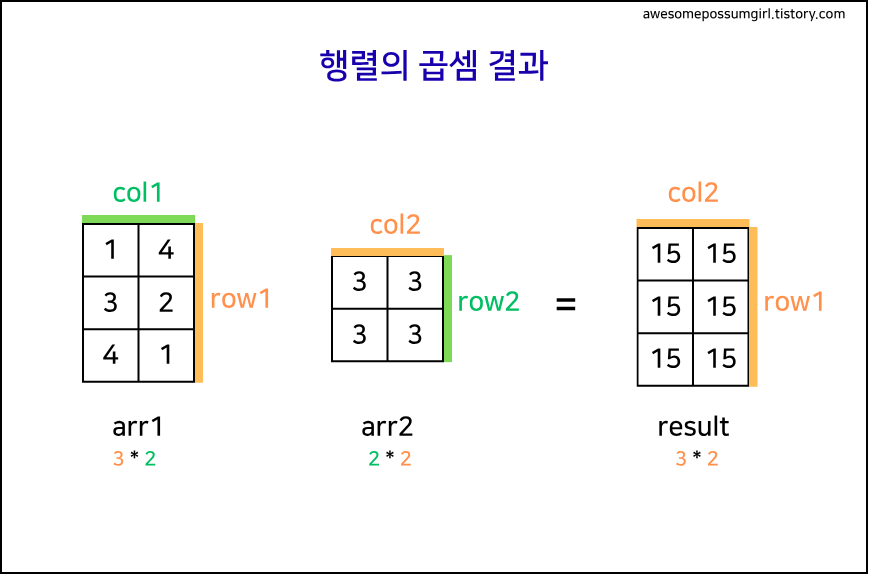
arr1 (3x2)        arr2 (2x2)          결과 (3x2)

[1, 4]         ×  [3, 3]         =    [15, 15]
[3, 2]            [3, 3]              [15, 15]
[4, 1]                                [15, 15]

곱셈은 이렇게 계산된다.

  • 결과[0][0]
    = 1×3 + 4×3 = 3 + 12 = 15
  • 결과[0][1]
    = 1×3 + 4×3 = 3 + 12 = 15
  • 결과[1][0]
    = 3×3 + 2×3 = 9 + 6 = 15
  • 결과[1][1]
    = 3×3 + 2×3 = 9 + 6 = 15
  • 결과[2][0]
    = 4×3 + 1×3 = 12 + 3 = 15
  • 결과[2][1]
    = 4×3 + 1×3 = 12 + 3 = 15

변수 3개 선언하는 이유

  • 각 위치 answer[i][j]는 arr1의 i행과 arr2의 j열을 곱해서 만든 결과이다.
  • 그래서 i, j, k 세 가지 기준이 필요해서 3중 for문이 되는 것이다.

아래는 결과 행렬의 크기를 만들기 위해 필요한 정보이다.

int row1 = arr1.length;        // arr1의 행 수 (결과 행)
int col1 = arr1[0].length;     // arr1의 열 수 (== arr2의 행 수, 곱셈 기준)
int col2 = arr2[0].length;     // arr2의 열 수 (결과 열)
  • row1은 arr1의 행 개수 → 결과 행렬의 행 수
  • col1은 행렬 곱할 때 내부 루프의 기준 (곱하고 더해야 하는 부분)
  • col2는 arr2의 열 개수 → 결과 행렬의 열 수

결과 행렬의 크기는 아래와 같다.

  • arr1: A × B (행 × 열)
  • arr2: B × C
  • ➜ 결과: A × C

그래서 결과 행렬을 new int[row1][col2] 로 만드는 것이다.

3중 for문 쓰는 이유

행렬 곱셈은 다음과 같이 정의된다. 

answer[i][j] = arr1[i][0]×arr2[0][j] + arr1[i][1]×arr2[1][j] + ... + arr1[i][k]×arr2[k][j]

즉, arr1의 i번째 행과 arr2의 j번째 열을 원소끼리 곱해서 모두 더해야 한다.

for (int i = 0; i < row1; i++) {          // arr1의 각 행 반복
    for (int j = 0; j < col2; j++) {      // arr2의 각 열 반복
        for (int k = 0; k < col1; k++) {  // arr1의 열 == arr2의 행
            answer[i][j] += arr1[i][k] * arr2[k][j];  // 원소끼리 곱해서 누적
        }
    }
}
  • i: 결과 행렬의 행 번호
  • j: 결과 행렬의 열 번호
  • k: 곱셈 대상 원소의 인덱스



Back to top