68. [Java] 정수를 나선형으로 배치하기
https://school.programmers.co.kr/learn/courses/30/lessons/181832
나선형으로 이차원 배열을 채운다는 것을 화살표로 표시 해 봤다.
입출력 예 #1번만 풀어서 단계별로 배열 변화 모습을 살펴 보면 아래와 같다.
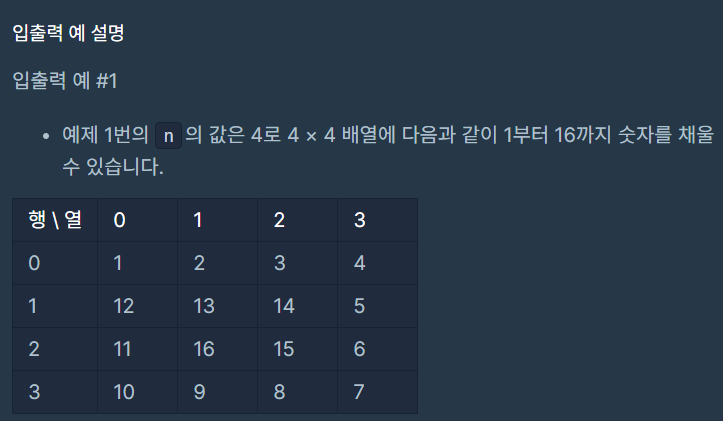
입출력 예 #1
초기 상태 (모두 0으로 비워진 상태)
[ 0, 0, 0, 0 ]
[ 0, 0, 0, 0 ]
[ 0, 0, 0, 0 ]
[ 0, 0, 0, 0 ]1. ➡ 오른쪽 (첫 줄 채우기)
[ 1, 2, 3, 4 ]
[ 0, 0, 0, 0 ]
[ 0, 0, 0, 0 ]
[ 0, 0, 0, 0 ]2. ⬇ 아래로
[ 1, 2, 3, 4 ]
[ 0, 0, 0, 5 ]
[ 0, 0, 0, 6 ]
[ 0, 0, 0, 7 ]3. ⬅ 왼쪽으로
[ 1, 2, 3, 4 ]
[ 0, 0, 0, 5 ]
[ 0, 0, 0, 6 ]
[ 10, 9, 8, 7 ]4. ⬆ 위로
[ 1, 2, 3, 4 ]
[ 0, 0, 0, 5 ]
[ 11, 0, 0, 6 ]
[ 10, 9, 8, 7 ]5. ➡ 오른쪽 (안쪽 한 줄)
[ 1, 2, 3, 4 ]
[ 12, 13, 14, 5 ]
[ 11, 0, 0, 6 ]
[ 10, 9, 8, 7 ]6. ⬇ 아래로
[ 1, 2, 3, 4 ]
[ 12, 13, 14, 5 ]
[ 11, 0, 15, 6 ]
[ 10, 9, 8, 7 ]7. ⬅ 왼쪽 (마무리)
[ 1, 2, 3, 4 ]
[ 12, 13, 14, 5 ]
[ 11, 16, 15, 6 ]
[ 10, 9, 8, 7 ]최종 결과 (n = 4)
[ 1, 2, 3, 4 ]
[ 12, 13, 14, 5 ]
[ 11, 16, 15, 6 ]
[ 10, 9, 8, 7 ]이렇게 4방향을 반복적으로 순환하면서 나선형을 만드는 구조이다. 이건 규칙을 찾기가 어려워서 일반적인 이중 for문으로는 해결이 어렵다.
그래서 상하좌우를 이동하는 방향 벡터 배열을 사용하는 게 핵심 포인트이다. 그래서 이 문제는 "좌표 이동" 문제로 본다. for문을 고정으로 돌리는 게 아니라, while문이나 for문 하나만 쓰면서 좌표를 업데이트하는 방식이다.
정답코드 (방향 벡터 배열)
class Solution {
public int[][] solution(int n) {
int[][] answer = new int[n][n];
// 방향: 오른쪽 → 아래 ↓ 왼쪽 ← 위 ↑
int[] dx = {0, 1, 0, -1}; // 행 이동
int[] dy = {1, 0, -1, 0}; // 열 이동
int x = 0, y = 0; // 시작 위치
int dir = 0; // 현재 방향 인덱스
int num = 1;
for (int i = 0; i < n * n; i++) {
answer[x][y] = num++;
// 다음 위치 계산
int nx = x + dx[dir];
int ny = y + dy[dir];
// 벽에 부딪히거나 이미 채운 곳이면 방향 전환
if (nx < 0 || nx >= n || ny < 0 || ny >= n || answer[nx][ny] != 0) {
dir = (dir + 1) % 4; // 방향 전환 (0→1→2→3→0 순환)
nx = x + dx[dir];
ny = y + dy[dir];
}
// 위치 이동
x = nx;
y = ny;
}
return answer;
}
}- 배열을 0으로 초기화한 n x n 배열을 만든다.
- 방향 배열을 설정하고, 현재 위치를 [0][0]으로 시작한다.
- 1부터 n^2까지 숫자를 채워 넣는다.
- 이동 방향을 따라 다음 좌표로 이동하면서, 범위 벗어나거나 이미 값이 있으면 방향을 바꾼다.
- 끝까지 반복한다.
✅ 방향 벡터 배열 (dx/dy 사용)
// 오른쪽 → 아래 ↓ 왼쪽 ← 위 ↑
int[] dx = {0, 1, 0, -1}; // 행 이동
int[] dy = {1, 0, -1, 0}; // 열 이동- 처음엔 오른쪽으로 가고,
- 막히면 아래로,
- 또 막히면 왼쪽으로,
- 또 막히면 위로...
- 방향 전환 조건이 핵심이다 - 배열 범위 초과하거나 이미 숫자가 있으면 방향을 꺾는다.
dir = (dir + 1) % 4로 방향을 순환시키면 나선형이 완성된다.
→ 왜냐하면 right -> down -> left -> up -> right 순으로 계속 순회하기 때문이다.
🔁 방향 전환 조건
방향을 바꿔야 하는 조건은 두 가지이다.
- 범위를 벗어날 때
- 이미 숫자가 들어있는 칸일 때
// 다음 위치가 범위를 벗어나거나, 이미 숫자가 들어있다면 방향 전환
if (nx < 0 || nx >= n || ny < 0 || ny >= n || arr[nx][ny] != 0) {
dir = (dir + 1) % 4;
}내가 푼 코드 (구간 조절 방식)
class Solution {
public int[][] solution(int n) {
int[][] answer = new int[n][n];
int num = 1;
int rowStart = 0, rowEnd = n - 1;
int colStart = 0, colEnd = n - 1;
while (rowStart <= rowEnd && colStart <= colEnd) {
// ➡ 오른쪽
for (int i = colStart; i <= colEnd; i++) {
answer[rowStart][i] = num++;
}
rowStart++;
// ⬇ 아래쪽
for (int i = rowStart; i <= rowEnd; i++) {
answer[i][colEnd] = num++;
}
colEnd--;
// ⬅ 왼쪽
for (int i = colEnd; i >= colStart; i--) {
answer[rowEnd][i] = num++;
}
rowEnd--;
// ⬆ 위쪽
for (int i = rowEnd; i >= rowStart; i--) {
answer[i][colStart] = num++;
}
colStart++;
}
return answer;
}
}구간 조절 방식
나처럼 해결하는 방법을 구간 조절 방식이라고 한다.
- 네 개의 경계선(rowStart, rowEnd, colStart, colEnd)을 설정하고, 이것을 점점 좁혀가면서 나선형으로 배열을 채우는 코드이다.
- 각 방향(오른쪽 → 아래 ↓ 왼쪽 ← 위 ↑)을 하나씩 직접 처리한다. 그래서 각 방향마다 for문을 따로 썼다.
- 이렇게 방향을 명확하게 코드로 명시하면 한 눈에 보기에도 쉽고 디버깅이 쉽다.
- 하지만 for문이 4개라서 코드 중복이 많고 방향이 4개 이상이 되는 경우는 유지보수도 어렵다.
방향 벡터 배열
- 그래서 구간 조절 방식 대신 일반적으로는 방향 벡터 배열 방식 (dx/dy 사용)이 권장 된다. - 상단 정답 코드 참고
- 방향 벡터 배열은 행이동 배열 dx, 열이동 배열 dy로 한 방향을 한 줄로 잡는 원리이다.
- 다음 위치가 범위를 벗어나거나 이미 채워졌으면 방향을 전환한다.
- 이건 코드가 짧고 유연하다. for문 하나로 4방향 모두 순회 가능하기 때문이다.
- 그래서 방향이 많거나 동적으로 바뀐는 문제제에 유리하다. 하지만 처음 보면 덜 직관적이고 구현 난이도가 어렵다.