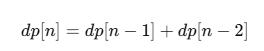Skip to main content

[Java] 12914 멀리 뛰기

📝 멀리 뛰기

1. 문제 요약

이 문제는 사실상 피보나치 수열이랑 똑같다 🙂

  • n = 1 → 1가지 방법 (1칸)
  • n = 2 → 2가지 방법 (1칸+1칸, 2칸)
  • n = 3 → 3가지 방법
  • n = 4 → 5가지 방법

점화식

image.png

이걸 매번 1234567로 나눈 나머지 저장하기

2. 정답코드

class Solution {
    public long solution(int n) {
        // n칸까지 방법 수 담을 배열
        long[] dp = new long[n + 1];
        
        dp[0] = 1; // 0칸일 때도 1가지 방법(아무것도 안함)
        dp[1] = 1; // 1칸일 때도 1가지 방법
        
        for (int i = 2; i <= n; i++) {
            dp[i] = (dp[i - 1] + dp[i - 2]) % 1234567;
        }
        
        return dp[n];
    }
}

공간최적화 - 배열 안쓰고 2칸만 기억

class Solution {
    public long solution(int n) {
        long a = 1, b = 1; // dp[0], dp[1]
        for (int i = 2; i <= n; i++) {
            long temp = (a + b) % 1234567;
            a = b;
            b = temp;
        }
        return b;
    }
}

3. 오답 / 어려웠던 점

​배열 칸 수 지정하는 부분이 헷갈렸다. 0부터 시작하는데 <= n까지인 이유

  • 칸 수 n 까지의 방법을 저장하려면 dp[n]까지 접근해야 한다.
  • 만약 배열 크기를 n으로 만들면 마지막 인덱스는 n-1 까지 밖에 안 된다.
  • 그래서 dp = new long[n + 1]로 만들면 dp[0] ~ dp[n]까지 접근 가능해져서 dp[n]을 바로 쓸 수 있다.
  • 예를 들어 n = 4 일 때
dp[0] = 1
dp[1] = 1
dp[2] = ?
dp[3] = ?
dp[4] = ?
  • n=4칸일 때, 칸을 0부터 4까지 있다고 생각한다.
  • 0칸 → 이미 출발점에 있음 → 방법 1가지
  • 1칸 → 1칸 뛰어서 도착 → 방법 1가지
  • 그럼 2칸, 3칸, 4칸 방법 수를 계산해야 된다.

이런 식으로 마지막 dp[4]까지 저장하려면 배열 길이가 5(n+1)이어야 함

dp[i] = i칸까지 도달하는 방법 수

  • 0칸: dp[0] = 1
  • 1칸: dp[1] = 1
  • 2칸: dp[2] = dp[1] + dp[0] = 1 + 1 = 2
  • 3칸: dp[3] = dp[2] + dp[1] = 2 + 1 = 3
  • 4칸: dp[4] = dp[3] + dp[2] = 3 + 2 = 5


Back to top