Skip to main content

[Java] 131701 연속 부분 수열 합의 개수

📝 연속 부분 수열 합의 개수

1. 문제 요약

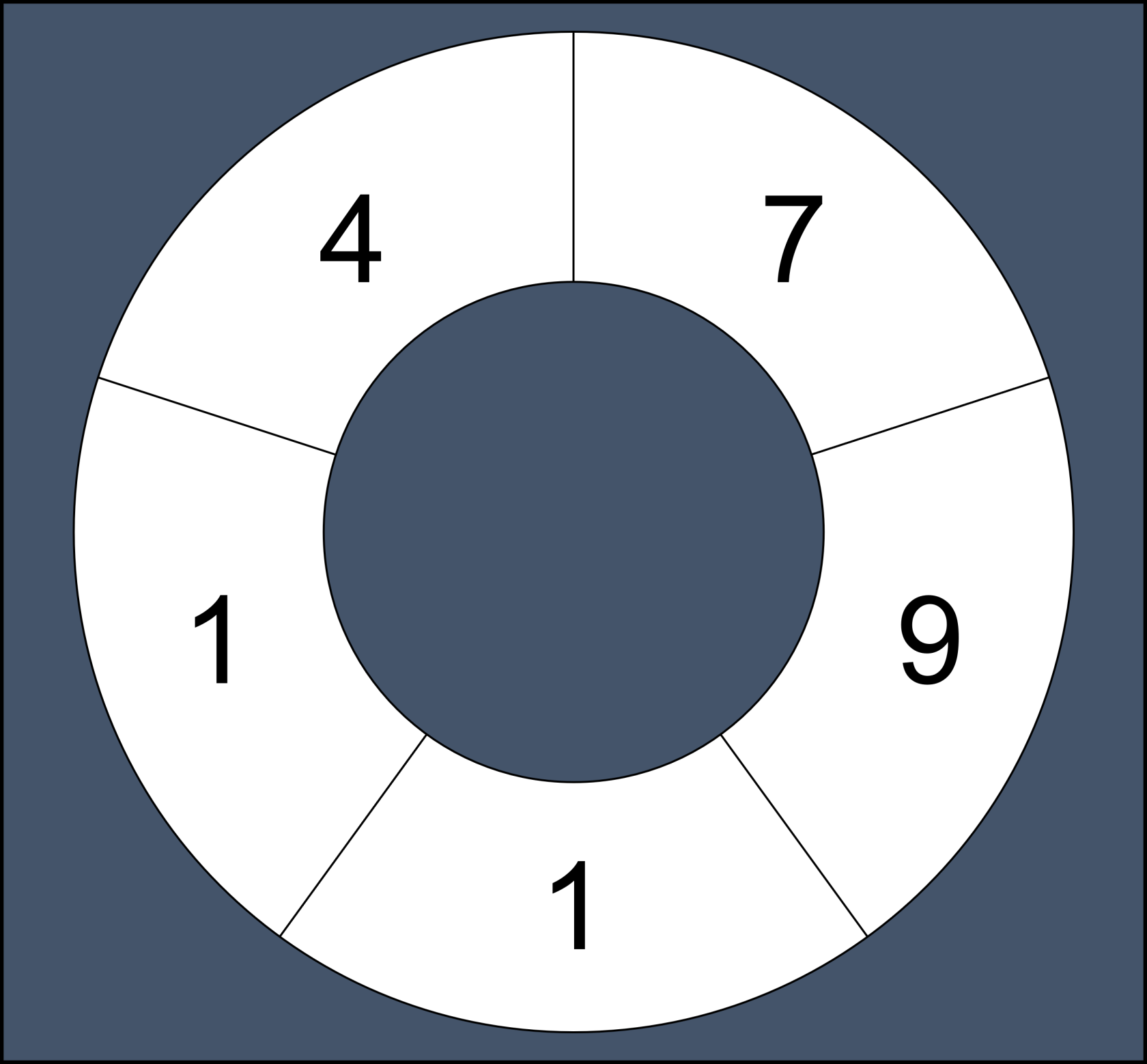
image.png

원형 수열 = 끝과 처음이 이어진 동그라미 배열

원형 수열을 구현한다는 건?

  • 배열 끝을 넘어가면 다시 청므으로 돌아가면서 합을 구하는 것
  • 배열 길이를 n이라고 하면, 인덱스를 계산할 때 항상 %n을 하면 됨
  • 배열 인덱스를 계산할 때 (start + i) % n을 쓰면 배열을 원형처럼 연결 할 수 있다.
    • 배열 : [7, 9, 1, 1, 4]
    • n = 5 (배열 길이)
    • start = 4 → 마지막 원소 4에서 시작
    • (4 + 1) % 5 = 0 → 배열 처음으로 돌아가서 연결됨
    • 이렇게 하면 배열 처음 원소 7로 돌아감


2. 정답코드

import java.util.*;

class Solution {
    public int solution(int[] elements) {
        int n = elements.length;
        Set<Integer> sums = new HashSet<>();
        
        // 길이 1부터 n까지 연속 부분 수열
        for (int len = 1; len <= n; len++) {
            for (int start = 0; start < n; start++) {
                int sum = 0;
                for (int i = 0; i < len; i++) {
                    sum += elements[(start + i) % n]; 
                }
                sums.add(sum);
            }
        }
        
        return sums.size();
    }
}

​각 길이마다, 각 시작점마다, 실제 합을 계산하기 위해 3중 for문을 쓴다.

  1. 첫번째 for문 (len)
    • 연속 부분 수열의 길이를 1부터 n까지 바꿔가며 검사한다.
    • 길이가 1, 2, 3, ... n인 모든 연속 부분 수열을 다 합쳐야 하니까 필요하다
  2. 두 번째 for문 (start)
    • 배열에서 부분 수열이 어디서 시작할 지 선택하는 부분이다
    • 길이가 len인 부분 수열에서 시작점이 되는 모든 인덱스가 start이다
  3. 세 번째 for문 (i)
    • 선택된 길이와 시작점 기준으로 실제 합을 계산한다
    • %n을 쓰는 이유는 배열이 원형이라고 가정했기 때문에, 끝까지 가면 다시 처음으로 돌아가기 위해서이다.
    • (start + i) % n

3. 오답 / 어려웠던 점

  1. 문제에서 중복 배제해야 함 따라서 Set 으로 풀어야 함.
  2. 처음에 원형 수열 구현하는 점화식 구하는게 어려웠다
  3. 3중 포문


Back to top