Skip to main content

[Java] 12924 숫자의 표현

1. 문제

숫자의 표현

2. 정답코드

등차수열

class Solution {
    public int solution(int n) {
        int count = 0;
        for (int k = 1 ; (k - 1) * k / 2 < n; k++) {
            int numerator = n - k * (k - 1) / 2;
            if (numerator % k == 0) {
                count++;
            }
        }

        return count;
    }
}

등차수열의 합 공식

  • 여기서는 숫자가 1 간격으로 늘어남
1 + 2 + 3 + ... + (k-1)
합 = (첫째 수 + 마지막 수) * 개수 / 2
  • 첫째 수 = 1
  • 마지막 수 = k-1
  • 개수 = (k-1)
1 + 2 + 3 + ... + (k-1) = (1 + (k-1)) * (k-1) / 2
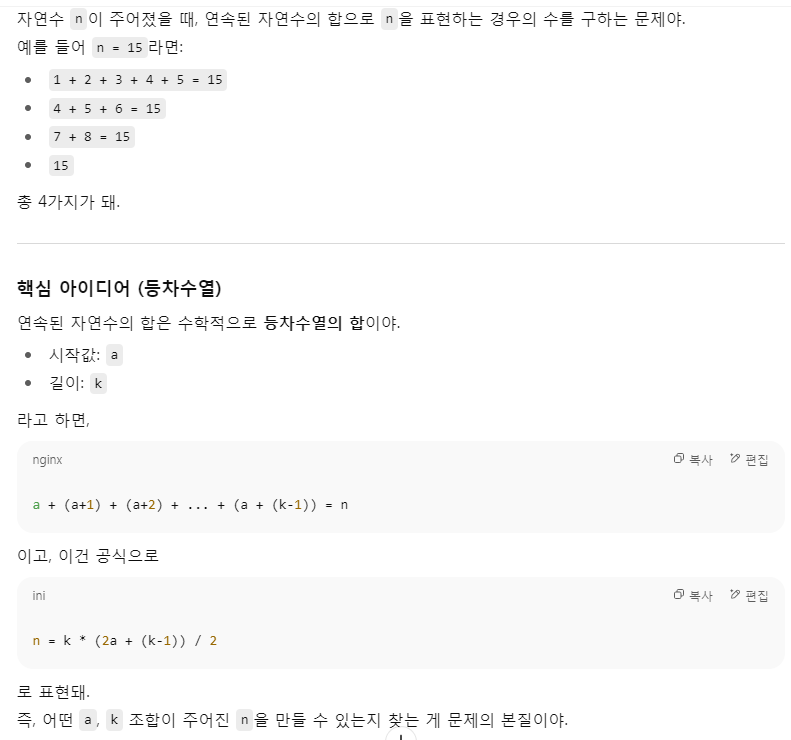
                           = k * (k-1) / 2
(k-1)*k/2

연속된 k개의 숫자를 더하면

x + (x+1) + ... + (x+k-1) = n

공식으로 바꾸면:

k*x + k*(k-1)/2 = n

x를 구하면:

x = (n - k*(k-1)/2) / k

여기서 k가 연속된 숫자의 개수이고 구한 x가 시작점

*    ****
**    ***
***    **
****    *

삼각형 두개 더하고 나누는 원리랑 같다

공식그대로 쓴 코드

이건 chatGPT에 물어봐서 내거보다 훨씬 간단한 코드

class Solution {
    public int solution(int n) {
        int count = 0;

        // k: 수열 길이
        for (int k = 1; k <= n; k++) {
            // 등차수열 합 공식: n = k * (2a + k - 1) / 2
            // 2n = k * (2a + k - 1)
            // 2a = (2n / k) - (k - 1)
            if ((2 * n - k * (k - 1)) % (2 * k) == 0) {
                count++;
            }
        }

        return count;
    }
}
  1. k는 수열의 길이(1, 2, 3, ...)
  2. 수열의 합 공식에서 a 계산하면
    2a = (2n / k) - (k - 1)
  3. a가 자연수인지 확인하기 (2n - k(k-1)) % (2*k) == 0
    나머지가 0이면 a가 정수 → 자연수 수열 존재
  4. 존재하면 count++

image.png

투포인터

class Solution {
    public int solution(int n) {
        int count = 0;
        int left = 1, right = 1, sum = 1;

        while (left <= n) {
            if (sum < n) {
                right++;
                sum += right;
            } else if (sum > n) {
                sum -= left;
                left++;
            } else { // sum == n
                count++;
                sum -= left;
                left++;
            }
        }

        return count;
    }
}
  1. left와 right를 연속 구간의 시작과 끝으로 둔다.
    1. 처음에는 left = 1, right = 1, sum = 1
  2. sum > n → 오른쪽 범위를 늘리고 (right++), 합 키우기
  3. sum < n → 왼쪽 범위 줄이고 (left++), 합을 줄여
  4. sum == n 이면 → 하나의 경우를 찾은 거니까 count++,
    그리고 계속 탐색하려고 left++ 하면서 다음 구간을 체크
  5. left가 n을 넘어가면 종료

왜 등차수열과 동일한지?

  • 투 포인터로 찾는 left ~ right 구간은 결국 연속된 자연수의 합
  • 즉, (left + (left + 1) + ... + right) 이런 꼴인데, 이게 바로 등차수열의 합


Back to top