Skip to main content

[Java] 340212 PCCP 2번 / 퍼즐 게임 챌린지

1. 문제

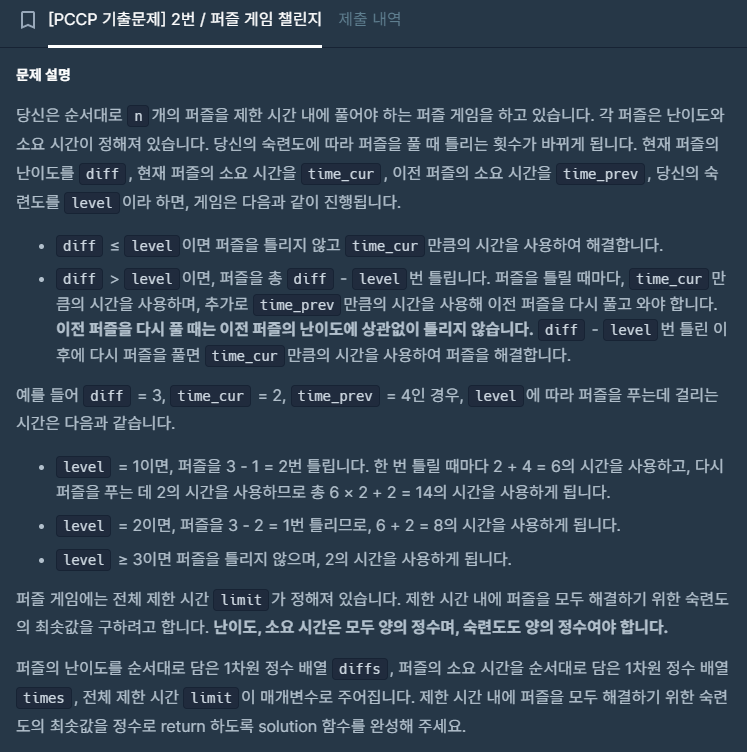
프로그래머스 [Java] [PCCP 기출문제] 2번 / 퍼즐 게임 챌린지

image.png

image.png

image.png

image.png

image.png

2. 접근 방법

퍼즐규칙

  1. 난이도(diff) <= 숙련도(level) → 한 번에 성공, 시간은 time_cur 소요
  2. 난이도(diff) > 숙련도 (level) → (diff - level) 번 실패
    • 실패 1회당 걸리는 시간 = time_cure + time_prev
    • 마지막 성공 = time_cur
  3. 퍼즐 하나 푸는데 걸리는 시간
// diff > level일 때
time = (diff - level) * (time_cur + time_prev) + time_cur 
// diff ≤ level일 때
time = time_cur

3. 오답코드

// diff > level일 때
// time = (diff - level) * (time_cur + time_prev) + time_cur 
// diff ≤ level일 때
// time = time_cur

class Solution {
    public int solution(int[] diffs, int[] times, long limit) {
        int level = 1;
        long leftTime = limit;
        // 0번 퍼즐 처리
        if (diffs[0] > level) {
            // 이전 퍼즐 없어서 times[-1] 생략
            leftTime -= (diffs[0] - level) * times[0]; 
        } else {
            leftTime -= times[0];
        }
        if (leftTime < 0) return level;
        level++;
        
        for (int i = 1; i < diffs.length; i++) {
            if (diffs[i] > level) {
                leftTime -= (diffs[i] - level) * (times[i] + times[i-1]) + times[i];     
            } else {
                leftTime -= times[i];    
            }
            if (leftTime < 0) return level;
            level++;
        }
        
        return level;
    }
}

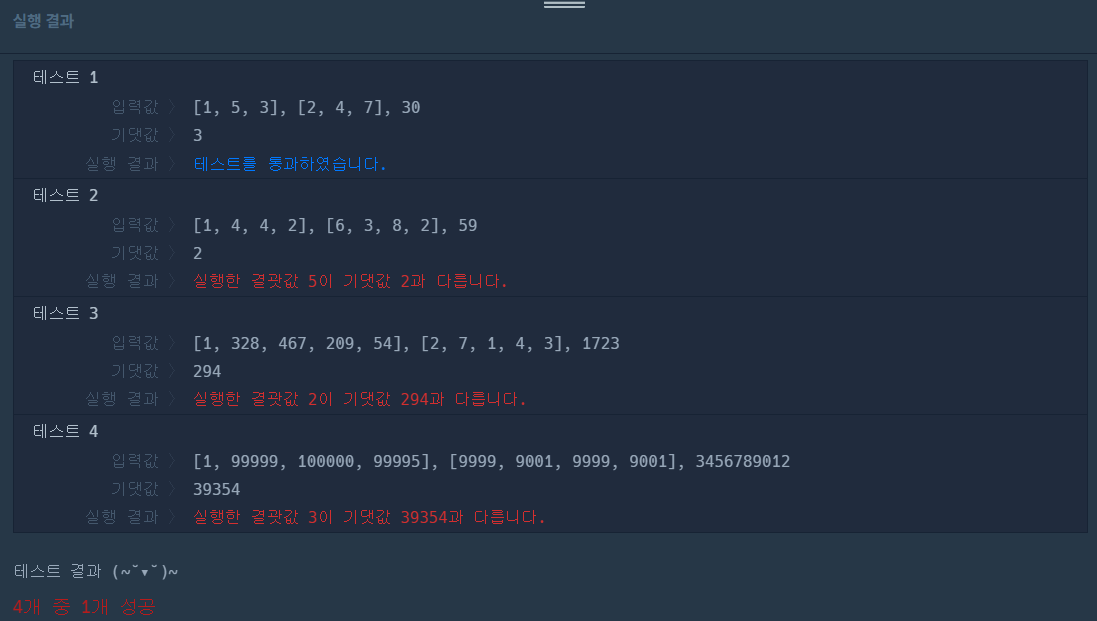
image.png

"퍼즐 다 풀 수 있는 최소 level"을 찾는 탐색 로직이 아니라 "어디까지 풀 수 있나"만 보는 시뮬레이션을 짜서 틀렸다.
이 문제는 총 시간이 level에 대해 단조적이므로, 이분 탐색 + 단일 시뮬레이션(check)으로 O(n log L)에 해결해야 한다.
문제의 핵심은 제한 시간 내에 모든 퍼즐을 풀 수 있는 최소 숙련도 level 를 찾는 것이다.

총 시간이 level에 대해 단조적이라는 말은 level 이 커질수록 총 소요 시간이 단조 감소(= 비증가) 한다는 뜻이다.
즉, 어떤 level 에서 제한 시간 안에 가능하다면, 그보다 큰 level 에서도 항상 가능하다.
이 성질 덕분에 “가능/불가능”을 판별하는 이분 탐색을 적용할 수 있다

해결방법

  • 이분탐색
  • 탐색 구간: level [1, max(diffs)] (최대 100,000)
  • 필요한 판별 함수 check(level): 주어진 level로 모든 퍼즐을 풀 때의 총 시간을 계산해 limit 이하인지만 판단한다.


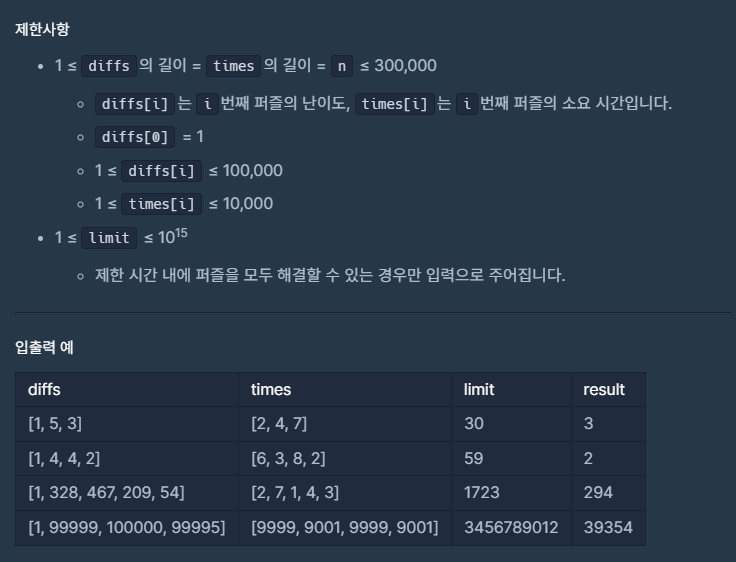
문제의 제한사항에서

  • 퍼즐 개수 n이 최대 300,000개,
  • 숙련도 level이 최대 100,000까지 주어질 수 있다.

라는 조건이 명시 되어 있다. 이 규모는 일반적인 제한 시간에서 절대 끝나기 어렵다는 뜻이다.

참고: 종종 “어차피 중간에 시간 초과 나면 멈춘다”라고 말하지만, 최악의 경우를 기준으로 보는 것이 시간복잡도 분석의 기본이다. 데이터가 빡빡하면 실제로도 최악에 가깝게 돈다.

내가 푼 방식대로라면 level 을 1부터 끝까지 올려가면서 매번 퍼즐 n개를 전부 시뮬레이션하는 선형 시뮬레이션을 돌리는데, 최악의 경우 100,000 × 300,000 = 30억 번 연산이 돌아간다. 이러면 시간 초과가 난다. 그래서 필요한 게 이분 탐색이다.


level 범위는 1 ~ 100,000인데, 이걸 check 함수를 만들어서 이분 탐색으로 줄이면 아래와 같다.

log2(100,000) ≈ 17
  • log₂(100,000) ≈ 16.6
  • 소수점 올려서 17이라고 표현한 것이다.
  • 즉, 이분 탐색은 최대 17번만 검사하면 1~100,000 구간을 전부 커버할 수 있다는 뜻이다.
  • 즉, 최대 17번만 check 함수를 호출하면 된다.
O(n) → 최대 17 × 300,000 = 510만 연산

이 정도면 충분히 시간 안에 돌아간다.


4. 정답코드

// diff > level일 때
// time = (diff - level) * (time_cur + time_prev) + time_cur 
// diff ≤ level일 때
// time = time_cur

class Solution {
    public int solution(int[] diffs, int[] times, long limit) {
        // 이분탐색
        int left = 1; 
        int right = 100000; // diff[i] 최댓값
        int answer = right;
        
        while (left <= right) {
            int mid = (left + right) / 2;
            if (canSolve(diffs, times, limit, mid)) {
                answer = mid;
                right = mid - 1; // 더 낮은 level 탐색
            } else {
                left = mid + 1; // 더 높은 level 필요
            }
            
        }
        
        return answer;
    }
    
    // 판별 메서드
    private boolean canSolve(int[] diffs, int[] times, long limit, int level) {
        long total = 0;
        
        // 0번 퍼즐
        if (diffs[0] > level) {
            total += (long)(diffs[0] - level) * times[0] + times[0];
        } else {
            total += times[0];
        }
        if (total > limit) return false;
        
        // 나머지 퍼즐
        for (int i = 1; i < diffs.length; i++) {
            if (diffs[i] > level) {
                total += (long)(diffs[i] - level) * (times[i] + times[i - 1])+ times[i];
            } else {
                total += times[i];
            }
            if (total > limit) return false;
        }
        
        return true;
    }
}

제한 시간 내에 퍼즐을 풀 수 있는 가장 최소 level을 탐색하는거니까 Lower Bound 이분탐색 알고리즘을 썼다.
최소 level을 찾기 위해 가능한 범위를 왼쪽으로 좁혀가는 방식이다.
처음에 right 범위를 diffs 의 max값으로 설정하고 절반씩 범위를 줄여가면서 만족하는 값을 찾는다.

canSolve(mid)

  • 주어진 숙련도 level로 제한 시간 안에 퍼즐을 다 풀 수 있는가를 true나 false로 반환하는 메서드
  • mid는 level이다.
  • true → 가능하니까 더 최소 level 값 탐색 → 왼쪽 구간 탐색 → right = mid -1
  • false → 불가능하니까 더 큰 level이 필요함 → 오른쪽 구간 탐색 → left = mid + 1
  • 이 때 누적시간이 int 범위 초과할 수 있어서 long 타입으로 변환해준다.


Back to top